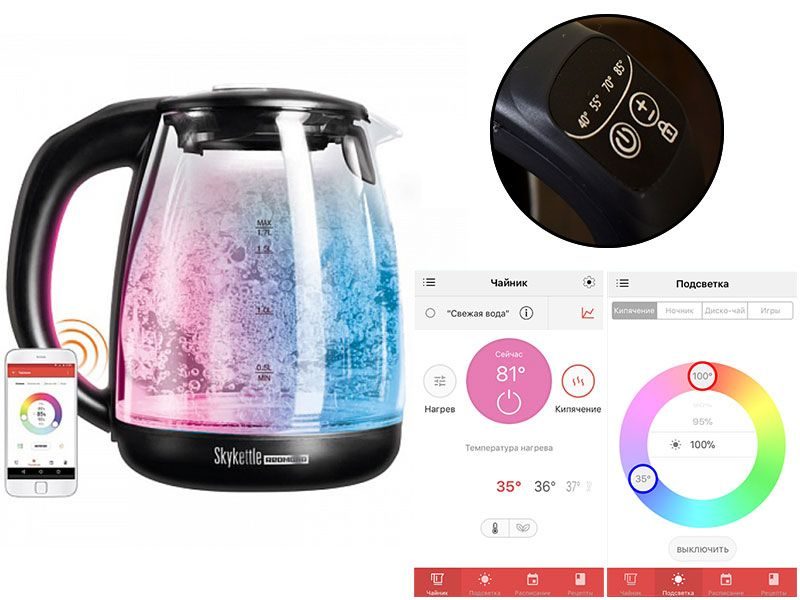
Измерительный мост
Измерительный мост, позволяющий определять величину неизвестного электрического сопротивления, был изобретён британским учёным Самуэлом Кристи в 1833 году, и позже модернизирован и популяризирован другим британским учёным, Чарьзом Витстоном в 1843 году.
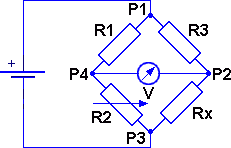
Схема измерительного моста Уинстона.
P1 – P3 – диагональ питания; P2 – P4 – измерительная диагональ моста;
R1, R2 – левое плечо, R3, Rx – правое плечо моста.
Принцип работы
Принцип измерения неизвестного сопротивления основан на уравнивании отношений сопротивлений в обоих плечах моста, при этом гальванометр, включённый между этими плечами, будет показывать нулевое напряжение. На рисунке Rx – это неизвестное сопротивление, которое требуется измерить. R1, R2 и R3 – резисторы с известными значениями сопротивлений, причём резистор R2 переменный. Если отношение двух известных сопротивлений в плече R2/R1 равно отношению сопротивлений в плече Rx/R3, то в этом случае напряжение между точками схемы P2 и P4 будет равно нулю, и через гальванометр V ток не будет течь. Если же мост разбалансирован, то отклонение гальванометра будут указывать на то, что сопротивление резистора R2 слишком большое или слишком маленькое. Переменный резистор R2 регулируют до тех пор, пока гальванометр не укажет на ноль.
По гальванометру можно определять отсутствие тока в цепи с очень большой точностью. Следовательно, если резисторы R1, R2 и R3 – высокоточные, то неизвестное сопротивление Rx может быть измерено с большой точностью. Небольшие изменения сопротивления Rx разбалансируют измерительный мост, что обнаруживается по показанию гальванометра.
При сбалансированном мосте выполняется равенство R2/R1 = Rx/R3.
Отсюда Rx = R3*R2 / R1
В случае если сопротивления R1, R2 и R3 известны, а резистор R2 – постоянный, то неизвестное сопротивление Rx может быть рассчитано с помощью законов Кирхгофа. Этот метод измерения часто используется при применении измерительного моста в тензометрии, совместно с тензодатчиком, так как считать показания с гальванометра получится гораздо быстрее, чем балансировать мост переменным резистором.
Расчёт
Используя первый закон Кирхгофа, найдём токи, протекающие в узлах P2 и P4:
Далее с помощью второго закона Кирхгофа найдём напряжения в контурах P1-P2-P4 и P2-P3-P4:
Мост сбалансирован, следовательно IG = 0, так что вторая система уравнений сократится:
Решая эту систему уравнений, получим:
Из первого закона Кирхгофа следует, что I3 = Ix и I1 = I2. Следовательно величина неизвестного сопротивления Rx будет определятся по формуле:
Если известны сопротивления всех четырёх резисторов и величина питающего напряжения Uпит, а сопротивление гальванометра достаточно высокое, так что током IG, протекающим через него можно пренебречь, то напряжение U между точками моста P2 и P4 может быть найдено путём расчёта каждого из делителей напряжения, вычтя затем напряжение на одном делителе из напряжения на другом делителе. В этом случае получится следующее уравнение:
Напряжение питания Uпит можно вынести за скобки, в этом случае получится выражение:
Где U – напряжение в точке P2 относительно точки P4.
Измерительный мост Уинстона иллюстрирует концепцию дифференциальных измерений, результаты которых могут быть очень точными. Различные разновидности моста Уинстона используются для измерения ёмкости, индуктивности, импеданса и других величин. Одной из разновидностей моста является мост Кельвина, специально предназначенный для измерения малых сопротивлений. Во многих случаях измерение величины неизвестного сопротивления связано с измерением некоторых физических параметров, таких как сила, температура, давление и т.д., здесь в качестве измеряемого сопротивления используется соответствующий резистивный датчик.
В 1865 году Джеймс Максвелл применил измерительный мост Уинстона, питаемый переменным током, для измерения индуктивности, и в 1926 году Алан Блюмлейн подверг этот мост усовершенствованию.
Модификации основной схемы измерительного моста
Мост Уинстона является основной схемой измерительных мостов, но так же существуют различные его модификации, с помощью которых можно проводить измерения различных типов сопротивлений, когда основная схема моста для этого не подходит. Вот несколько разновидностей основной схемы измерительного моста:
Применение моста Уитстона для измерения неэлектрических величин
Мост Уитстона представляет собой электрическую схему, предназначенную для измерения величины электрического сопротивления. Впервые данная схема была предложена британским физиком Самуэлем Кристи в 1833 году, а в 1843 году она была усовершенствована изобретателем Чарльзом Уитстоном. Принцип работы данной схемы схож с действием механических аптекарских весов, только уравниваются здесь не силы, а электрические потенциалы.
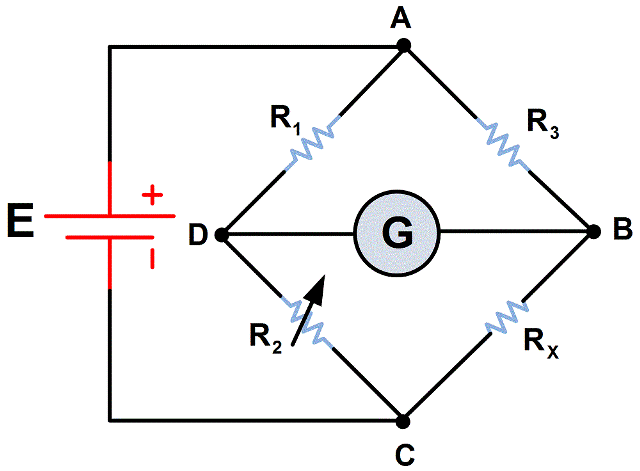
Схема моста Уитстона содержит две ветви, потенциалы средних выводов (D и B) которых уравниваются в процессе проведения измерений. Одна из ветвей моста включает в себя резистор Rx, значение сопротивления которого необходимо определить.
Противоположная ветвь содержит реостат R2 — сопротивление регулируемой величины. Между средними выводами ветвей включен индикатор G, в качестве которого может выступать гальванометр, вольтметр, нуль-индикатор или амперметр.
В ходе измерительного процесса сопротивление реостата постепенно изменяют до тех пор, пока индикатор не покажет ноль. Это значит, что потенциалы средних точек моста, между которыми он включен, равны друг другу, и разность потенциалов между ними равна нулю.
Когда стрелка индикатора (гальванометра) отклонена в ту или иную сторону от нуля, это значит что через него протекает ток, и следовательно мост еще не находится в балансе. Если же на индикаторе ровно ноль — мост сбалансирован.
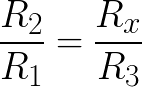
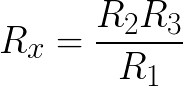
Очевидно, если отношение верхнего и нижнего сопротивлений в левом плече моста равно отношению сопротивлений правого плеча моста — наступает баланс (или равновесие) моста просто в силу нулевой разности потенциалов между выводами гальванометра.
И если значения трех сопротивлений моста (включая текущее сопротивление реостата) сначала измерены с достаточно небольшой погрешностью, то искомое сопротивление Rx будет найдено с достаточно высокой точностью. Считается что сопротивлением гальванометра можно пренебречь.

Мост Уитстона по сути универсален, и применим отнюдь не только для измерений сопротивлений резисторов, но и для нахождения самых разных неэлектрических параметров, достаточно лишь чтобы сам датчик неэлектрической величины был резистивным.
Тогда сопротивление чувствительного элемента-датчика, изменяясь под неэлектрическим воздействием на него, может быть измерено при помощи мостовой схемы Уитстона, и соответствующая неэлектрическая величина может быть таким образом найдена с малой погрешностью.
Таким образом можно найти значение величины: механической деформации (тензометрические датчики), температуры, освещенности, теплопроводности, теплоемкости, влажности, и даже состав вещества.
Современные измерительные приборы на базе моста Уитстона обычно снимают показания с моста через аналого-цифровой преобразователь, подключенный к цифровому вычислительному устройству, такому как микроконтроллер с вшитой программой, которая осуществляет линеаризацию (замена нелинейных данных приближенными линейными), масштабирование и преобразование полученных данных в численное значение измеряемой неэлектрической величины в соответствующих единицах измерения, а также коррекцию погрешностей и вывод в читаемом цифровом виде.

Например напольные весы примерно по такому принципу и работают. Кроме того программными методами тут же может быть проведен гармонический анализ и т. д.

Так называемые тензорезисторы (резистивные датчики механического напряжения) находят применение в электронных весах, в динамометрах, манометрах, торсиометрах и тензометрах.
Тензорезистор просто наклеивается на деформируемую деталь, включается в плечо моста, при этом напряжение в диагонали моста будет пропорционально механическому напряжению, на которое реагирует датчик — его сопротивление изменяется.
При разбалансе моста измеряют величину этого разбаланса, и таким образом находят например вес какого-нибудь тела. Датчик, кстати, может быть и пьезоэлектрическим, если измеряется быстрая или динамическая деформация.

Когда необходимо измерить температуру, применяются резистивные датчики, сопротивление которых изменяется вместе с изменением температуры исследуемого тела или среды. Датчик может даже не контактировать с телом, а воспринимать тепловое излучение, как это происходит в болометрических пирометрах.
Принцип действия болометрического пирометра основан на изменении электрического сопротивления термочувствительного элемента вследствие его нагревания под воздействием поглощаемого потока электромагнитной энергии. Тонкая пластинка из платины, зачерненная для лучшего поглощения излучения, из-за своей малой толщины под действием излучения быстро нагревается и ее сопротивление повышается.
Похожим образом действуют термометры сопротивления с положительным температурным коэффициентом и терморезисторы с отрицательным температурным коэффициентом на базе полупроводников.

При изменении температуры косвенным путем можно измерить теплопроводность, теплоемкость, скорость потока жидкости или газа, концентрацию компонентов газовой смеси и т. д. Именно косвенные измерения такого рода применяются в газовой хроматографии и в термокаталитических датчиках.


Фоторезисторы изменяют свое сопротивление под действием освещенности, а для измерения потоков ионизирующего излучения – используются специализированные резистивные датчики.
Измерительный мост Уитстона и его использование
Одной из популярнейших мостовых схем, по сей день применяемых в контрольно-измерительных приборах и в электротехнических лабораториях, является измерительный мост Уитстона, названный в честь английского изобретателя Чарльза Уитстона, предложившего данную схему для измерения сопротивлений в далеком 1843 году.

Измерительный мост Уитстона является по сути электрическим аналогом аптекарских рычажных весов, так как здесь используется подобный компенсационный метод измерения.
Принцип действия измерительного моста основан на уравнивании потенциалов средних выводов двух включенных параллельно ветвей резисторов, в каждой ветви по два резистора. В качестве части одной из ветвей включается резистор, величину которого требуется узнать, а в другую — резистор перестраиваемого сопротивления (реостат или потенциометр).
Плавно изменяя величину сопротивления перестраиваемого резистора, добиваются нулевого показания на шкале гальванометра, включенного в диагональ между средними точками двух упомянутых ветвей. В условиях, когда гальванометр покажет ноль, потенциалы средних точек будет равны, и значит можно легко вычислить искомое сопротивление.
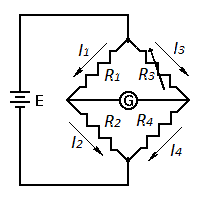
Понятно, что кроме резисторов и гальванометра, в схеме обязательно должен присутствовать источник питания моста, на приведенном рисунке он изображен в виде гальванического элемента Е. Ток течет от плюса батарейки к минусу, при этом делится между двумя ветвями обратно пропорционально их сопротивлениям.
Если верхние и нижние резисторы в плечах моста попарно одинаковы, то есть когда плечи полностью идентичны, нет причин для возникновения тока через диагональ, поскольку разность потенциалов между точками подключения гальванометра равна нулю. В этом случае говорят что мостик уравновешен или сбалансирован.
Если же верхние резисторы одинаковы, а нижние не одинаковы, то ток устремится через диагональ, от плеча с большим нижним сопротивлением к плечу с меньшим нижним сопротивлением, и стрелка гальванометра отклонится в соответствующую сторону.
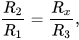
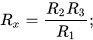
Итак, если потенциалы точек, к которым подключен гальванометр, равны, то соотношения номиналов верхних и нижних резисторов в плечах будут равны между собой. Таким образом, приравняв эти соотношения, получим уравнение с одним неизвестным. Сопротивления R1, R2 и R3 должны быть изначально измерены с высокой точностью, тогда и точность нахождения резистора Rх(R4) будет высокой.
Схему моста Уитстона часто используют для измерения температуры, когда в одну из ветвей моста включают термометр сопротивления в качестве неизвестного резистора. В любом случае, чем больше разность сопротивлений в ветвях, тем больший ток будет течь через диагональ, а при изменении сопротивлений станет изменяться и ток диагонали.
Именно это свойство моста Уитстона так ценится теми, кто решает задачи контрольно-измерительного характера и разрабатывает схемы управления и автоматизации. Малейшее изменение сопротивления в одной из ветвей приводит к изменению тока через мостик, и это изменение фиксируется. Вместо гальванометра в диагональ моста можно включить амперметр или вольтметр, в зависимости от конкретной схемы и цели исследования.

Вообще, с помощью моста Уитстона можно измерять самые разные величины: упругую деформацию, освещенность, влажность, теплоемкость и т. д., достаточно лишь вместо измеряемого резистора включить в схему соответствующий датчик, чувствительный элемент которого будет способен изменять свое сопротивление в соответствии с изменением измеряемой величины, пусть даже не электрической. Как правило, мост Уитстона подключается в таких случаях через АЦП, а дальнейшая обработка сигнала, отображение информации на дисплее, действия с опорой на получаемые данные — все это остается делом техники.
Принцип работы моста уитстона
Электрический ток. Сила тока. Плотность тока
Непрерывное направленное движение электрических зарядов называют электрическим током.
Ток может течь в твердых телах, жидкостях и газах. Если среда является проводником с большим количеством свободных электронов, то течение электрического тока осуществляется за счет дрейфа этих электронов. Дрейф электронов в проводниках, не связанный с перемещением вещества, называют током проводимости.
Различают ток проводимости и конвекционный ток. Количественной характеристикой электрического тока являются сила тока I и плотность j .
Сила тока — скалярная величина, равная отношению количества электричества dq, которое за время dt, переносится через данное сечение проводника, к времени dt :
| . | (1) |
|---|
Постоянным называют электрический ток, сила и направление которого с течением времени не изменяются. Для постоянного тока
| . | (2) |
|---|
Плотность тока — векторная физическая величина, модуль которой равен отношению силы тока I к площади поперечного сечения проводника S :
| . | (3) |
|---|
Вектор j направлен вдоль направления тока, т. е. совпадает с направлением упорядоченного движения положительных зарядов.
Закон Ома. Сопротивление проводников.
Для того чтобы в проводнике все время шел ток, необходимо поддерживать в нем постоянное электрическое поле, т.е. на концах проводника должна быть постоянная разность потенциалов.
Сила тока в проводнике пропорциональна напряжению на его концах и обратно пропорциональна сопротивлению проводника (закон Ома для участка цепи):
| . | (4) |
|---|
Сопротивление проводников зависит от материала проводника, т. е. строения его кристаллической решетки. Для однородного цилиндрического проводника длиной l и площадью поперечного сечения S сопротивление определяется по формуле
| . | (5) |
|---|
где r — удельное сопротивление проводника. Единица удельного сопротивления — омметр (Ом•м).
Величина g=1/R , обратная сопротивлению, называется проводимостью. Единица электрической проводимости — Сименс (См).
Величина g =1/ r , обратная удельному сопротивлению, называется удельной электрической проводимостью проводника. Единица удельной электрической проводимости — (См/м).
Закон Ома можно представить в дифференциальной форме
| . | (6) |
|---|
Выражение (6), связывающее плотность тока в любой точке внутри проводника с напряженностью электрического поля в этой же точке
Обобщённый закон Ома имеет вид
| . | (7) |
|---|
где j 1 и j 2 – потенциалы в начальной и конечной точках участка, e – ЭДС, R – сопротивление участка, I – ток на участке цепи.
В замкнутой цепи ЭДС источника тока равна сумме падений напряжений на внешнем и внутреннем участках цепи, так как при перемещении по замкнутой цепи заряд возвращается в исходное положение — в точку с тем же потенциалом. Тогда
| . | (8) |
|---|
ЭДС, как и сила тока, — величина алгебраическая. Если ЭДС способствует движению положительных зарядов в выбранном направлении, то она считается положительной. Если ЭДС препятствует движению положительных зарядов, то она считается отрицательной. Соединение источников в батарею может быть последовательным и параллельным.
Соединение проводников. Зависимость сопротивления проводников от температуры
Проводники в электрической цепи могут соединяться последовательно (рис.1) или параллельно (рис.2).
Рис. 1. Последовательное соединение проводников
При последовательном соединении сила тока во всех частях одинакова. Общее напряжение равно сумме напряжений на отдельных участках:
| . |
Отсюда следует, что общее сопротивление цепи, состоящей из последовательно соединенных проводников, равно сумме сопротивлений отдельных проводников:
| . | (9) |
|---|
При параллельном соединении проводников сила тока в неразветвленной части цепи равна сумме сил токов, текущих в параллельных участках:
Рис. 2. Параллельное соединение проводников
| . |
Падения напряжения в параллельно соединенных участках одинаковы.
Отсюда следует что, общее сопротивление R параллельно соединенных проводников цепи рассчитывается следующим образом:
| . | (10) |
|---|
Удельное электрическое сопротивление проводника зависит не только от рода вещества, но и от его состояния. Зависимость удельного сопротивления r от температуры имеет вид:
| . |
где r 0 – удельное сопротивление при 0°С; t – температура (по шкале Цельсия); a – температурный коэффициент сопротивления, характеризующий относительное изменение сопротивления проводника при нагревании его на 1°С или 1K:
Температурные коэффициенты сопротивления веществ различны при разных температурах. Однако для многих металлов изменение a с температурой не очень велико. Для всех чистых металлов a» 1/273 1/К (или 1/°С).
Правила Кирхгофа
В общем случае на практике часто приходится рассчитывать сложные разветвленные электрические цепи, содержащие узлы (рис.3).
Рис. 3. Соединение проводников в узел
Узлом А в разветвленной цепи называют точку, в которой сходится не меньше трех проводников.
Алгебраическая сумма токов, сходящихся в узле, равна нулю (первое правило Кирхгофа):
| . | (11) |
|---|
Токи, подходящие к узлу, считаются положительными, а отходящие — отрицательными.
Обобщением закона Ома является второе правило Кирхгофа, оно относится к любому замкнутому контуру разветвленной электрической цепи: в любом замкнутом контуре разветвленной цепи алгебраическая сумма ЭДС равна алгебраической сумме произведений токов на сопротивления соответствующих участков этого контура:
| . | (12) |
|---|
где m — число участков в замкнутом контуре, n — число источников тока в этом контуре.
Если при решении уравнений сила тока получилась отрицательной, то необходимо изменить условное направление этого тока на противоположное, сохраняя найденное значение силы тока неизменным.
Мост Уитстона
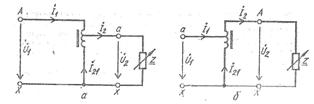
Для точных измерений сопротивлений в лабораторных условиях широко применяются мосты постоянного тока. Мостовая схема изображена на (рис.4). Сопротивления R 1 , R 2 , R 3 и R 4 называются плечами моста. В диагональ ab моста включается источник постоянного напряжения, в диагональ cd – измерительный прибор (обычно гальванометр магнитоэлектрической системы).
Рис. 4. Мостовая схема
Мост называется уравновешенным, если потенциалы точек c и d равны при подключении источника питания. При этом стрелка гальванометра стоит на нуле.
Для уравновешенного моста справедливы следующие соотношения: I 1 R 1 =I 3 R 3 , I 2 R 2 =I 4 R 4 и I 1 =I 2 , I 3 =I 4 . Отсюда
| . |
Если R 1 =R x неизвестное сопротивление, а R 2 , R 3 , R 4 образованы магазинами сопротивлений то
| . | (13) |
|---|
Уравновешенный мост позволяет измерять сопротивления с большой точностью.
| . |
где L 1 и L 2 – длины плеч ad и db соответственно.
Измерительные мосты постоянного и переменного тока. Принципы измерений: мост Уитстона
При обслуживании металлических кабельных линий наиболее часто пользуются измерительными мостами, хотя для поиска мест повреждения кабеля существуют и другие приборы. Во-первых, они обеспечивают высокую точность в широком диапазоне измеряемых величин. Во-вторых, их применение позволяет организовать измерения таким образом, чтобы компенсировать посторонние влияния, что незаменимо для локализации неисправности. В-третьих, они недороги.
Учитывая сказанное, полезно ознакомиться не только с устройством измерительных мостов, но и с принципами их применения для локализации неисправностей. Впрочем, говоря языком математики, для построения оптимальных схем измерения такие знания необходимы, но недостаточны. Диагностика – это всегда и опыт, и искусство.
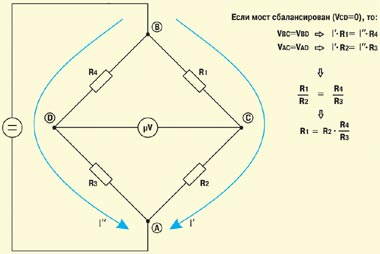
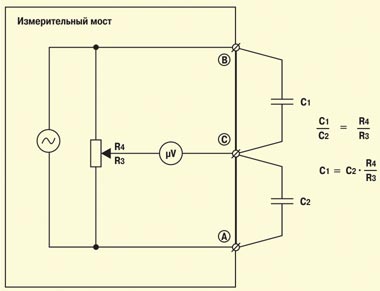
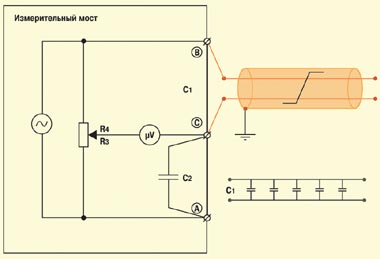
Принцип работы мостовой схемы измерения продемонстрировано на Рисунке 1 (RM1a), а способ ее применения на практике – на Рисунке 2 (RM2a). Сопротивление R1 вычисляется исходя из полученного при балансировке моста соотношения R4/R3, в качестве R2 используется резистор с известным значением. Конечно, сказанное дает только самое общее представление об измерительной схеме моста. На самом деле он устроен гораздо сложнее – современные мосты создаются на основе цифровых процессоров. Микропроцессорное ядро позволяет автоматизировать процедуру измерения (в первых моделях оператор должен был пользоваться калькулятором, сегодня же все расчеты выполняются аппаратурой), обеспечить многофункциональность устройства (многие мосты интегрированы с другими измерительными приборами – мультиметрами, рефлектометрами и т. п.), устранить помехи (посторонние постоянные и переменные напряжения почти всегда присутствуют на жилах кабелей), организовать дальнейшую обработку накопленных результатов измерений (хранение, обмен с компьютером, печать протоколов) и др.
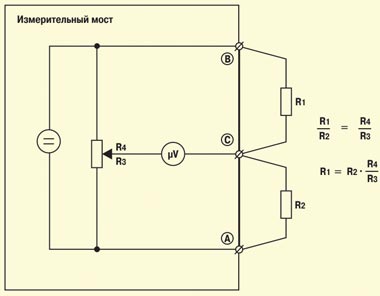
Рассмотренный выше мост, используемый для измерения сопротивления, носит имя Уитстона (Wheatstone). Для подключения измеряемых цепей в нем применяются всего две клеммы (B и C). Более сложные схемы реализованы в двух других мостах – Муррея (Murray) и Купфмюллера (Kupfmuller) (RM2в). Здесь измеряемые цепи подключаются с помощью трех клемм (A, B и C). В более сложных схемах Хиборна/Графа (Hilborn/Graf) задействуются четыре клеммы (A, B, B’ и C) (RM3). Смысл увеличения числа точек подключения станет понятен при рассмотрении схем измерения с применением мостов.
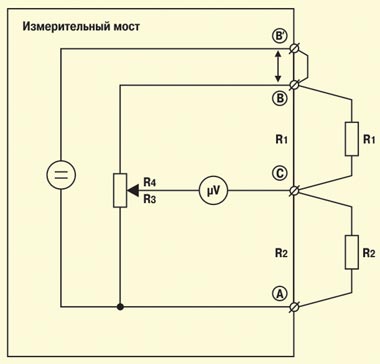
Еще один момент. Все упомянутые мостовые схемы используются для измерений при постоянном токе (определяются величины активных сопротивлений, подключенных к клеммам). Кроме того, мостовые схемы Уитстона и Муррея используются для измерений при переменном токе (определяются величины емкостей, подключенных к клеммам). В таких мостах источником напряжения служит генератор синусоидального напряжения.
Теперь остановимся на схемах измерений. С помощью моста Уитстона при постоянном токе измеряют сопротивление витой пары (шлейфа), сопротивление изоляции жил пары, сопротивление изоляции между жилами и экраном (RM3, RM4, RM5).
Значения упомянутых параметров используются для диагностики кабельных линий. Локализация же неисправностей требует определения места повреждения на кабельной линии. При помощи моста постоянного тока несложно вычислить расстояние до места повреждения. Зная сопротивление шлейфа Rшл и погонное сопротивление жил кабеля Rпог, можно воспользоваться формулой: Lпары = Rшл / 2Rпог, и рассчитать длину витой пары.
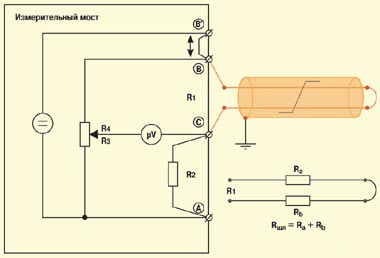
Погонное сопротивление медных жил определяется табличным способом по их сечению. Оно зависит не только от сечения жил, но и от их температуры. Чтобы избежать ошибки, нужно использовать значение погонного сопротивления для соответствующей температуры (особенно важно это для воздушных кабельных линий, где температура меняется в широких пределах). В простых мостах значения вводятся оператором вручную из таблиц. В более сложных приборах при помощи автоматической или полуавтоматической калибровочной процедуры определяется поправочный коэффициент по измеренному значению температуры (для чего в комплекте прибора присутствует щуп-датчик).
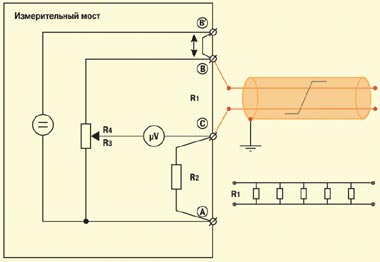
Длина витой пары может быть установлена также мостовым методом при переменном токе. В таком случае измеряемым параметром является емкость витой пары. Разделив емкость витой пары на ее погонную емкость, получим длину витой пары.
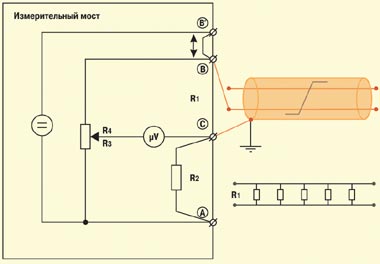
Аналогично рассмотренным выше измерениям при постоянном токе, с помощью моста Уитстона при переменном токе определяются емкость витой пары (шлейфа) и емкость каждой из жил пары относительно экрана. Длина жил может быть вычислена по их погонной емкости. Погонная емкость (нФ/км) витой пары зависит от сечения жил, типа скрутки, вида и материала изоляции и определяется табличным способом по типу кабеля.
Резкое увеличение емкости витой пары по сравнению с ее паспортным значением, как правило, свидетельствует о наличии воды в сердечнике кабеля. Для локализации повреждений этого типа применяются другие методы, прежде всего зондирование поврежденной пары с помощью рефлектометра.
Отметим, что, в отличие от сопротивления, погонная емкость слабо зависит от температуры, что существенно упрощает измерения.
Измерительный мост

Измерительный мост – электрическая схема, усовершенствованная английским физиком Чарльзом Уинстоном. Она источник постоянного тока и базовая мостовая схема, которую применяют в конструкциях многих измерительных приборов. Например, в устройствах контроля и измерения температур – термометрах.
Что такое измерительный мост?
Как пример, объясняющий электросхему моста, возьмём терморезистор или термометр. В таких системах механизм ставят в одной ветви схемы. Можно провести аналогию с аптечными весами. Разница только в том, что мост – электрическое устройство.
Рычажные весы и приборы с мостовой схемой действуют компенсационным способом. Величина тока в по Уинстону есть разница между сопротивлениями – чем она выше, тем обширнее протекает электрический ток. При изменении разности меняется и количество электрических зарядов.
Это свойство применяют в различных системах и приборах контроля. Точность замеров достигается за счет изменения сопротивления. Во время измерения электричества, проходящего через измерительный мост постоянного тока, обнаруживаются любые изменения физической величины сопротивления.
Принцип работы моста Уитстона
Мостовая схема Ч. Уинстона состоит из 2-х плеч. В каждом 2 резистора. Соединяет 2 параллельные ветви еще одна. Ее название – мостик. Ток проходит от клеммы с минусом к верхнему пику мостовой схемы.
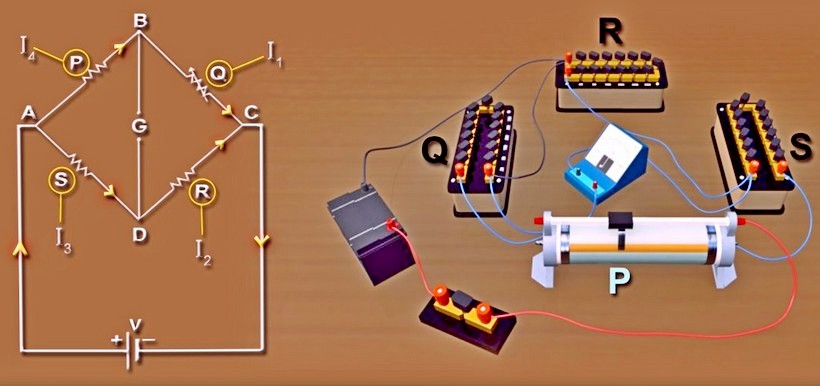
Разделившись по 2 параллельным ветвям, ток идёт к положительной клемме. Величина сопротивления в каждой ветви непосредственно влияет на количество тока. Равное сопротивление на обеих ветвях говорит о том, что в них течет аналогичное количество тока. В таких условиях мостовой элемент уравновешен.
Если в ветвях неравное сопротивление, ток в электросхеме начинает движение от ветви с высоким уровнем сопротивления к ветви с наименьшим. Так продолжается, пока 2 верхних элемента цепей остаются равны по своей величине. Аналогичное положение резисторы имеют в схемах, которые используют в системах контроля и измерения.
Типы и модификации измерительных мостов
Основная схема измерительного моста – Уинстона. Одинарный мост меряет сопротивление от 1 Ом до 100 Мом. Но есть и модификации, позволяющие измерять разные типы сопротивлений – те, для которых базовая схема не годится.
Разновидности
- Небольшие сопротивления измеряются посредством прибора Кери Фотера. Можно узнать разницу между противодействиями больших значений.
- Еще один тип – делитель Кельвина-Варлея. Применяется в приборах лабораторного оборудования. Максимальная измеряющая способность, зафиксированная этим делителем напряжения, достигает 1,0*10-7.
- Мост Кельвина, который в некоторых странах называют именем Томсона, предназначен для замера неизвестных сопротивлений небольших величин (меньше 1 Ом). По принципу работы похож на одинарный мост Уинстона. Разница лишь в наличии дополнительного сопротивления, снижающего погрешности в измерении, которые появляются в результате падения напряжения в одном из плеч.
- Еще один тип – мост Максвелла. Измеряет низкодобротную индуктивность неизвестной величины.
Схемы измерительных мостов
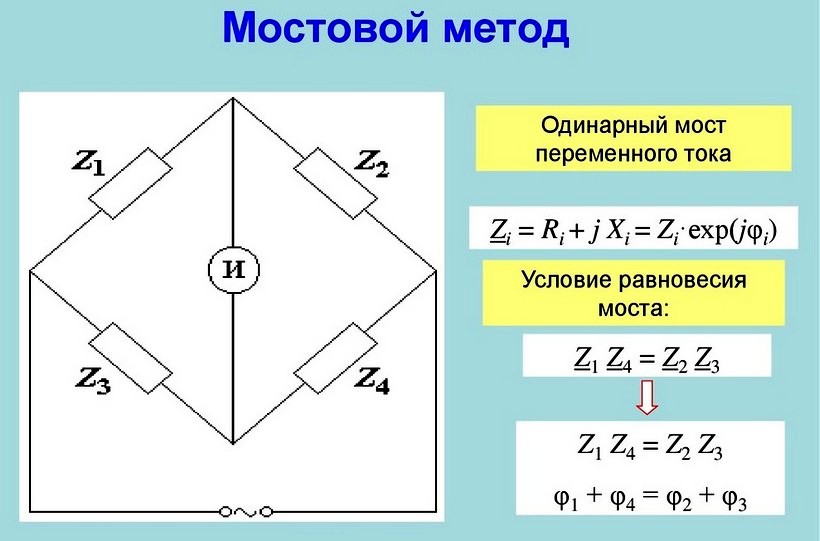
Измерительные мосты переменного тока делят на 2 группы: двойные и одинарные. Одинарные имеют 4 плеча. В них 3 ветви создают цепь с 4 точками подключения.
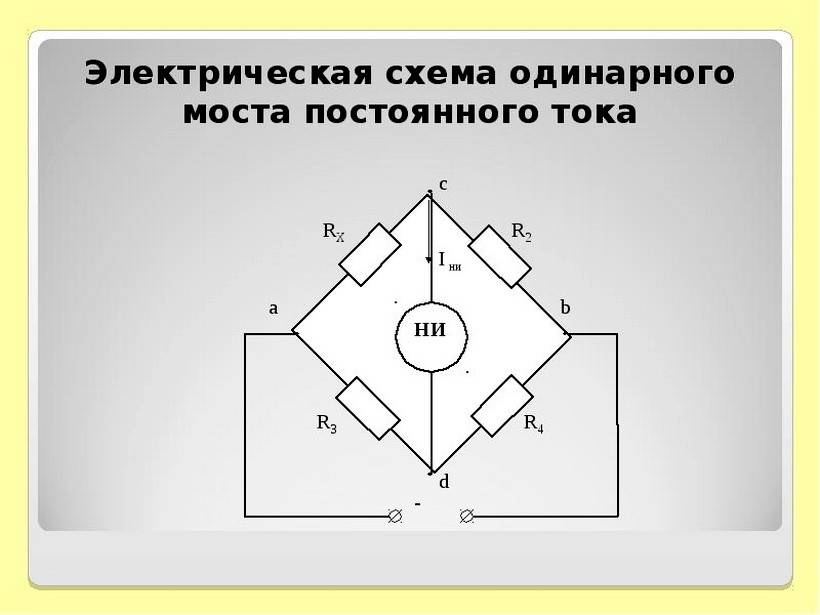
В диагонали моста есть электромагнитный гальванометр, показывающий равновесие. В другой диагонали моста действует источник постоянного питания. Измерения могут происходить с погрешностями, которые зависят от их диапазона. По мере роста сопротивления чувствительность прибора уменьшается.
Двойной мост называют шестиплечим. Его плечи – измеряемое сопротивление (Rx), резистор (Ro) и 2 пары дополнительных резисторов (Rl, R2, R3, R4).
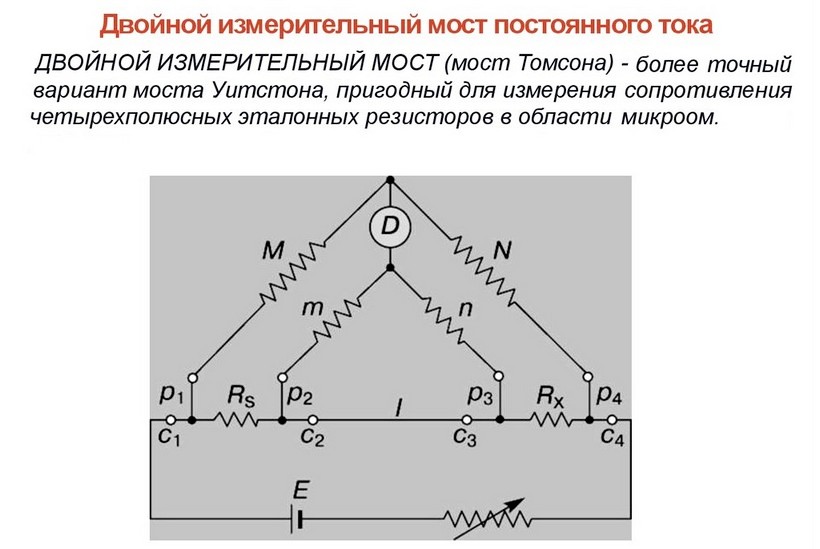
Двойные измерительные мосты
Небольшие сопротивления измеряются двойными мостами, состоящими из таких компонентов:
- резисторы R (4);
- гальванометр;
- резистор образцовый;
- источник питания;
- амперметр;
- резистор, устанавливающий рабочий ток.
Чтобы узнать условия, при которых возникает равновесие, для замкнутых контуров применяют уравнение Кирхгофа. Соблюдается условие: по гальванометру должен идти нулевой ток.
Где используют измерительный мост Уитстона?
Измерительные элементы применяют в работе с кабельными линиями из металла. Они позволяют нейтрализовать постороннее влияние для более эффективной локализации дефектов. Гарантированы высокоточные результаты в рамках диапазона измеряемых величин.
С помощью мостовой схемы Уитстона можно вычислить сопротивление изменяющегося элемента. Схемы используют в конструкциях электронных весов, электронных термометров и терморезисторов.
Среди промышленных образцов широко известны приборы с ручной калибровкой равновесия:
- ММВ – измеряет сопротивление проводника постоянного напряжения;
- Р333 – схема одинарного моста, с помощью которой выявляется поврежденный участок кабеля.

Заключение
С помощью прибора Уинстона можно мерить индуктивность, содержание газа в воздухе или другом веществе, емкость и иные физические величины. Подробно о данных схемах можно прочитать в учебнике «Измерительные соединения». В книге представлены основные понятия, базовые методики, примеры, иллюстрирующие принцип действия.