Мост уитстона принцип действия

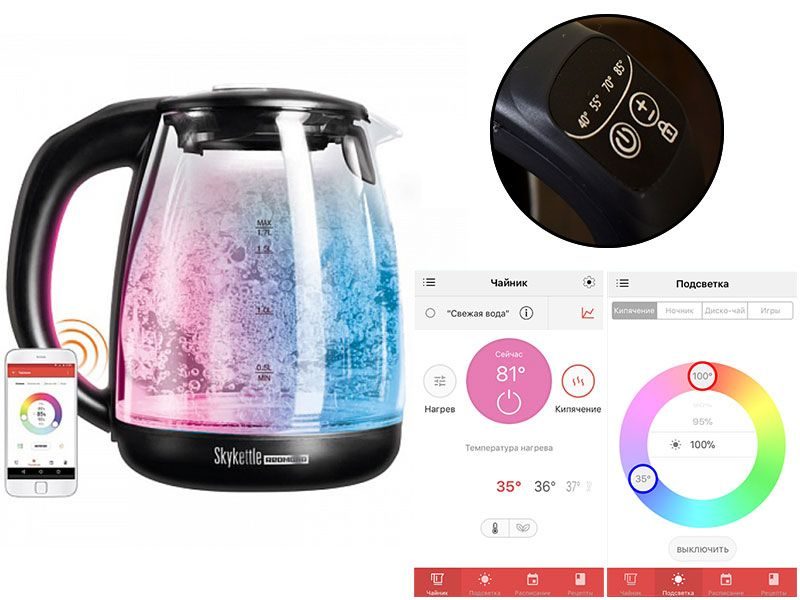
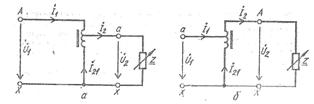
Измерительный мост Уитстона и его использование

Одной из популярнейших мостовых схем, по сей день применяемых в контрольно-измерительных приборах и в электротехнических лабораториях, является измерительный мост Уитстона, названный в честь английского изобретателя Чарльза Уитстона, предложившего данную схему для измерения сопротивлений в далеком 1843 году.

Измерительный мост Уитстона является по сути электрическим аналогом аптекарских рычажных весов, так как здесь используется подобный компенсационный метод измерения.

Принцип действия измерительного моста основан на уравнивании потенциалов средних выводов двух включенных параллельно ветвей резисторов, в каждой ветви по два резистора. В качестве части одной из ветвей включается резистор, величину которого требуется узнать, а в другую — резистор перестраиваемого сопротивления (реостат или потенциометр).

Плавно изменяя величину сопротивления перестраиваемого резистора, добиваются нулевого показания на шкале гальванометра, включенного в диагональ между средними точками двух упомянутых ветвей. В условиях, когда гальванометр покажет ноль, потенциалы средних точек будет равны, и значит можно легко вычислить искомое сопротивление.

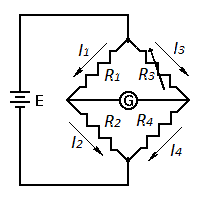
Понятно, что кроме резисторов и гальванометра, в схеме обязательно должен присутствовать источник питания моста, на приведенном рисунке он изображен в виде гальванического элемента Е. Ток течет от плюса батарейки к минусу, при этом делится между двумя ветвями обратно пропорционально их сопротивлениям.

Если верхние и нижние резисторы в плечах моста попарно одинаковы, то есть когда плечи полностью идентичны, нет причин для возникновения тока через диагональ, поскольку разность потенциалов между точками подключения гальванометра равна нулю. В этом случае говорят что мостик уравновешен или сбалансирован.

Если же верхние резисторы одинаковы, а нижние не одинаковы, то ток устремится через диагональ, от плеча с большим нижним сопротивлением к плечу с меньшим нижним сопротивлением, и стрелка гальванометра отклонится в соответствующую сторону.

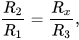
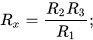
Итак, если потенциалы точек, к которым подключен гальванометр, равны, то соотношения номиналов верхних и нижних резисторов в плечах будут равны между собой. Таким образом, приравняв эти соотношения, получим уравнение с одним неизвестным. Сопротивления R1, R2 и R3 должны быть изначально измерены с высокой точностью, тогда и точность нахождения резистора Rх(R4) будет высокой.

Схему моста Уитстона часто используют для измерения температуры, когда в одну из ветвей моста включают термометр сопротивления в качестве неизвестного резистора. В любом случае, чем больше разность сопротивлений в ветвях, тем больший ток будет течь через диагональ, а при изменении сопротивлений станет изменяться и ток диагонали.

Именно это свойство моста Уитстона так ценится теми, кто решает задачи контрольно-измерительного характера и разрабатывает схемы управления и автоматизации. Малейшее изменение сопротивления в одной из ветвей приводит к изменению тока через мостик, и это изменение фиксируется. Вместо гальванометра в диагональ моста можно включить амперметр или вольтметр, в зависимости от конкретной схемы и цели исследования.

Вообще, с помощью моста Уитстона можно измерять самые разные величины: упругую деформацию, освещенность, влажность, теплоемкость и т. д., достаточно лишь вместо измеряемого резистора включить в схему соответствующий датчик, чувствительный элемент которого будет способен изменять свое сопротивление в соответствии с изменением измеряемой величины, пусть даже не электрической. Как правило, мост Уитстона подключается в таких случаях через АЦП, а дальнейшая обработка сигнала, отображение информации на дисплее, действия с опорой на получаемые данные — все это остается делом техники.

Применение моста Уитстона для измерения неэлектрических величин

Мост Уитстона представляет собой электрическую схему, предназначенную для измерения величины электрического сопротивления. Впервые данная схема была предложена британским физиком Самуэлем Кристи в 1833 году, а в 1843 году она была усовершенствована изобретателем Чарльзом Уитстоном. Принцип работы данной схемы схож с действием механических аптекарских весов, только уравниваются здесь не силы, а электрические потенциалы.

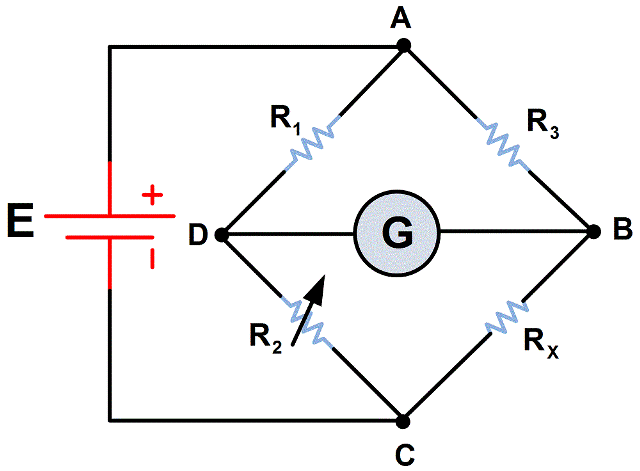
Схема моста Уитстона содержит две ветви, потенциалы средних выводов (D и B) которых уравниваются в процессе проведения измерений. Одна из ветвей моста включает в себя резистор Rx, значение сопротивления которого необходимо определить.

Противоположная ветвь содержит реостат R2 — сопротивление регулируемой величины. Между средними выводами ветвей включен индикатор G, в качестве которого может выступать гальванометр, вольтметр, нуль-индикатор или амперметр.

В ходе измерительного процесса сопротивление реостата постепенно изменяют до тех пор, пока индикатор не покажет ноль. Это значит, что потенциалы средних точек моста, между которыми он включен, равны друг другу, и разность потенциалов между ними равна нулю.

Когда стрелка индикатора (гальванометра) отклонена в ту или иную сторону от нуля, это значит что через него протекает ток, и следовательно мост еще не находится в балансе. Если же на индикаторе ровно ноль — мост сбалансирован.

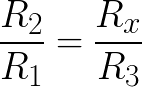
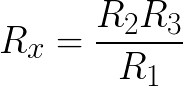
Очевидно, если отношение верхнего и нижнего сопротивлений в левом плече моста равно отношению сопротивлений правого плеча моста — наступает баланс (или равновесие) моста просто в силу нулевой разности потенциалов между выводами гальванометра.

И если значения трех сопротивлений моста (включая текущее сопротивление реостата) сначала измерены с достаточно небольшой погрешностью, то искомое сопротивление Rx будет найдено с достаточно высокой точностью. Считается что сопротивлением гальванометра можно пренебречь.

Мост Уитстона по сути универсален, и применим отнюдь не только для измерений сопротивлений резисторов, но и для нахождения самых разных неэлектрических параметров, достаточно лишь чтобы сам датчик неэлектрической величины был резистивным.

Тогда сопротивление чувствительного элемента-датчика, изменяясь под неэлектрическим воздействием на него, может быть измерено при помощи мостовой схемы Уитстона, и соответствующая неэлектрическая величина может быть таким образом найдена с малой погрешностью.

Таким образом можно найти значение величины: механической деформации (тензометрические датчики), температуры, освещенности, теплопроводности, теплоемкости, влажности, и даже состав вещества.

Современные измерительные приборы на базе моста Уитстона обычно снимают показания с моста через аналого-цифровой преобразователь, подключенный к цифровому вычислительному устройству, такому как микроконтроллер с вшитой программой, которая осуществляет линеаризацию (замена нелинейных данных приближенными линейными), масштабирование и преобразование полученных данных в численное значение измеряемой неэлектрической величины в соответствующих единицах измерения, а также коррекцию погрешностей и вывод в читаемом цифровом виде.

Например напольные весы примерно по такому принципу и работают. Кроме того программными методами тут же может быть проведен гармонический анализ и т. д.

Так называемые тензорезисторы (резистивные датчики механического напряжения) находят применение в электронных весах, в динамометрах, манометрах, торсиометрах и тензометрах.

Тензорезистор просто наклеивается на деформируемую деталь, включается в плечо моста, при этом напряжение в диагонали моста будет пропорционально механическому напряжению, на которое реагирует датчик — его сопротивление изменяется.

При разбалансе моста измеряют величину этого разбаланса, и таким образом находят например вес какого-нибудь тела. Датчик, кстати, может быть и пьезоэлектрическим, если измеряется быстрая или динамическая деформация.

Когда необходимо измерить температуру, применяются резистивные датчики, сопротивление которых изменяется вместе с изменением температуры исследуемого тела или среды. Датчик может даже не контактировать с телом, а воспринимать тепловое излучение, как это происходит в болометрических пирометрах.

Принцип действия болометрического пирометра основан на изменении электрического сопротивления термочувствительного элемента вследствие его нагревания под воздействием поглощаемого потока электромагнитной энергии. Тонкая пластинка из платины, зачерненная для лучшего поглощения излучения, из-за своей малой толщины под действием излучения быстро нагревается и ее сопротивление повышается.

Похожим образом действуют термометры сопротивления с положительным температурным коэффициентом и терморезисторы с отрицательным температурным коэффициентом на базе полупроводников.

При изменении температуры косвенным путем можно измерить теплопроводность, теплоемкость, скорость потока жидкости или газа, концентрацию компонентов газовой смеси и т. д. Именно косвенные измерения такого рода применяются в газовой хроматографии и в термокаталитических датчиках.

Фоторезисторы изменяют свое сопротивление под действием освещенности, а для измерения потоков ионизирующего излучения – используются специализированные резистивные датчики.

Измерительный мост

Измерительный мост, позволяющий определять величину неизвестного электрического сопротивления, был изобретён британским учёным Самуэлом Кристи в 1833 году, и позже модернизирован и популяризирован другим британским учёным, Чарьзом Витстоном в 1843 году.

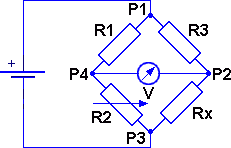
Схема измерительного моста Уинстона.
P1 – P3 – диагональ питания; P2 – P4 – измерительная диагональ моста;
R1, R2 – левое плечо, R3, R_x – правое плечо моста.

Принцип работы

Принцип измерения неизвестного сопротивления основан на уравнивании отношений сопротивлений в обоих плечах моста, при этом гальванометр, включённый между этими плечами, будет показывать нулевое напряжение. На рисунке R_x – это неизвестное сопротивление, которое требуется измерить. R1, R2 и R3 – резисторы с известными значениями сопротивлений, причём резистор R2 переменный. Если отношение двух известных сопротивлений в плече R2/R1 равно отношению сопротивлений в плече R_x/R3, то в этом случае напряжение между точками схемы P2 и P4 будет равно нулю, и через гальванометр V ток не будет течь. Если же мост разбалансирован, то отклонение гальванометра будут указывать на то, что сопротивление резистора R2 слишком большое или слишком маленькое. Переменный резистор R2 регулируют до тех пор, пока гальванометр не укажет на ноль.

По гальванометру можно определять отсутствие тока в цепи с очень большой точностью. Следовательно, если резисторы R1, R2 и R3 – высокоточные, то неизвестное сопротивление R_x может быть измерено с большой точностью. Небольшие изменения сопротивления R_x разбалансируют измерительный мост, что обнаруживается по показанию гальванометра.

При сбалансированном мосте выполняется равенство R2/R1 = R_x/R3.

Отсюда R_x = R3*R2 / R1

В случае если сопротивления R1, R2 и R3 известны, а резистор R2 – постоянный, то неизвестное сопротивление R_x может быть рассчитано с помощью законов Кирхгофа. Этот метод измерения часто используется при применении измерительного моста в тензометрии, совместно с тензодатчиком, так как считать показания с гальванометра получится гораздо быстрее, чем балансировать мост переменным резистором.

Расчёт

Используя первый закон Кирхгофа, найдём токи, протекающие в узлах P2 и P4:

Далее с помощью второго закона Кирхгофа найдём напряжения в контурах P1-P2-P4 и P2-P3-P4:

Мост сбалансирован, следовательно I_G = 0, так что вторая система уравнений сократится:

Решая эту систему уравнений, получим:

Из первого закона Кирхгофа следует, что I₃ = I_x и I₁ = I₂. Следовательно величина неизвестного сопротивления R_x будет определятся по формуле:

Если известны сопротивления всех четырёх резисторов и величина питающего напряжения U_пит, а сопротивление гальванометра достаточно высокое, так что током I_G, протекающим через него можно пренебречь, то напряжение U между точками моста P2 и P4 может быть найдено путём расчёта каждого из делителей напряжения, вычтя затем напряжение на одном делителе из напряжения на другом делителе. В этом случае получится следующее уравнение:

Напряжение питания U_пит можно вынести за скобки, в этом случае получится выражение:

Где U – напряжение в точке P2 относительно точки P4.

Измерительный мост Уинстона иллюстрирует концепцию дифференциальных измерений, результаты которых могут быть очень точными. Различные разновидности моста Уинстона используются для измерения ёмкости, индуктивности, импеданса и других величин. Одной из разновидностей моста является мост Кельвина, специально предназначенный для измерения малых сопротивлений. Во многих случаях измерение величины неизвестного сопротивления связано с измерением некоторых физических параметров, таких как сила, температура, давление и т.д., здесь в качестве измеряемого сопротивления используется соответствующий резистивный датчик.

В 1865 году Джеймс Максвелл применил измерительный мост Уинстона, питаемый переменным током, для измерения индуктивности, и в 1926 году Алан Блюмлейн подверг этот мост усовершенствованию.

Модификации основной схемы измерительного моста

Мост Уинстона является основной схемой измерительных мостов, но так же существуют различные его модификации, с помощью которых можно проводить измерения различных типов сопротивлений, когда основная схема моста для этого не подходит. Вот несколько разновидностей основной схемы измерительного моста:

Мост Уитстона (мост постоянного тока)

Компенсационный способ измерения сопротивлений является наиболее точным. Принципиальная схема метода (мост Уитстона) дана на рис. 5. Мостовая схема представляет собой замкнутый четырехугольник abcd, составленный из сопротивлений R₁, R₂, R₃, R₄, называемых плечами моста. Противоположные вершины ас и bd соединены диагоналями моста. В одну диагональ включен источник тока, в другую – нулевой гальванометр Г. При некотором соотношении между сопротивлениями плеч ток, протекающий через гальванометр, обращается в ноль (i_g = 0). В этом случае говорят, что мост уравновешен.

Условие равновесия моста. Обозначим токи в плечах соответственно через i₁ , i₂ , i₃ , i₄ . Так как i_g = 0, то, во-первых, i₁ = i₂ , а i₃ = i₄ и, во-вторых, φ_b = φ_d . По закону Ома разности потенциалов для плеч равны:

Это и есть условие равновесия моста. Его используют для расчета одного из 4-х сопротивлений. Пусть вместо R₁ в цепь включен резистор с неизвестным сопротивлением R_X . При трех остальных известных сопротивлениях

Таким образом, измерение неизвестного сопротивления сводится к уравновешиванию моста с тремя известными и одним неизвестным сопротивлением и расчета последнего по формуле (7).

Уравновесить мост, т.е. добиться отсутствия тока через гальванометр, можно двумя способами. Во-первых, установив постоянное отношение R₃ / R₄, подбирать соответствующее сопротивление R₂ и, во-вторых, установив постоянное сопротивление R₂, изменять отношение плеч R₃ / R₄. Первый способ используется в декадных мостах. Второй способ реализуется в линейных мостах (рис. 6). Здесь R_Х – неизвестное сопротивление, R₂ – магазин сопротивлений. Сопротивления R₃ и R₄ заменены отрезками l₃ и l₄ калиброванной проволоки (реохорда). Перемещая движок D вдоль реохорда, можно плавно изменять отношения плеч R₃ / R₄ . Так как сопротивление проволоки пропорционально длине, то отношение сопротивлений R₃ / R₄ можно заменить отношением соответствующих отрезков реохорда l₃/l₄ . Таким образом, измерение неизвестного сопротивления сводится к следующему:

1. Замыкая на короткое время кнопку К и перемещая движок D вдоль реохорда, следует добиться равновесия моста (при замкнутом ключе К ток через гальванометр не течет i_g = 0).

2. Определить по линейке реохорда длины отрезков l₃ и l₄ = l – l₃ , где l – длина всего реохорда.

3. Рассчитать неизвестное сопротивление по формуле:

Для повышения точности измерений следует стремиться к тому, чтобы мост был уравновешен при отношении плеч l₃/l₄ близком к 1, т.е. чтобы движок D находился примерно в средней трети длины реохорда. Для этого сопротивление R₂ должно быть приблизительно равно R_Х . Если сопротивление R_Х неизвестно даже приблизительно, то, выбрав R₂ произвольно, уравновешивают мост и рассчитывают R_Х сначала приближенно, а затем, установив на магазине сопротивлений R₂ » R_Х, повторяют измерения и рассчитывают R_Х более точно.

Поскольку сопротивление реохорда мало, мост Уитстона описанного типа применяется, как правило, для измерения небольших сопротивлений (от 1 до 1000 Ом).

Не нашли то, что искали? Воспользуйтесь поиском:

Лучшие изречения: Да какие ж вы математики, если запаролиться нормально не можете. 8624 – | 7456 – или читать все.

194.79.20.244 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.

Отключите adBlock!
и обновите страницу (F5)
очень нужно

Мост уитстона принцип действия

Мостовые схемы

Никакой учебник по электроизмерительным приборам нельзя назвать полным, если в нем не будет раздела, посвященного мостовым схемам. Эти гениальные схемы используют индикатор нулевого баланса (детектор “нуля”) для сравнения двух напряжений. Но, в отличие от “потенциометрических” схем, которые используются только для измерения неизвестного напряжения, мостовые схемы могут быть использованы для измерения всех видов электрических величин, включая и сопротивление.

Стандартная мостовая схема, часто называемая мостом Уитстона, выглядит примерно так:

Когда напряжение между точкой 1 и минусом батареи равно напряжению между точкой 2 и отрицательным выводом батареи, то индикатор баланса будет показывать ноль, и про такой мост говорят что он “сбалансирован”. Состояние баланса моста полностью зависит от отношений R_a/R_b и R₁/R₂, и оно не зависит от напряжения питания. Для измерения сопротивлений с помощью моста Уитстона на место резисторов R_a или R_b устанавливается неизвестное сопротивление, в то время как остальные три резистора являются прецизионными и их номинал известен. Каждый из этих трёх резисторов может быть заменён сопротивлением другой величины или их номиналы могут быть скорректированы, что бы мост сбалансировался, и когда это произойдёт то величина сопротивления неизвестного резистора может быть определена из соотношения величин известных сопротивлений.

Для этого необходимо, что бы измерительная система имела набор переменных резисторов с точно известными значениями, которые могут служить эталонными стандартами. Например, если мост настроен на измерение сопротивления R_x (рисунок 2), то мы должны знать точное значение остальных трёх сопротивлений при сбалансированном мосте, что бы определить величину сопротивления R_x:

Каждое из четырёх сопротивлений в мостовой схеме называют плечом. Резистор, последовательно соединённый с неизвестным сопротивлением, R_x обычно называют реостатом моста (это будет сопротивление R_a на рисунке 2), а другие два сопротивления называют плечами отношений моста.

Точные и стабильные образцовые сопротивления к счастью, не сложно изготовить. В действительности они были одними из первых электрических “Стандартных” устройств, изготовленных в научных целях. Ниже приведена фотография старинного блока стандартных сопротивлений:

Стандарт сопротивлений, изображённый на этой фотографии, является переменным с дискретным шагом изменения сопротивления: величина сопротивления между клеммами может изменяться в зависимости от количества и положения медных вставок, вставленных в разъёмы.

Мосты Уитстона считаются превосходным средством измерения сопротивления среди схем различных омметров. Но в отличие от всех этих схем, являющихся нелинейными (и имеющих нелинейные шкалы), и связанные с этим погрешности измерений, мостовая схема является линейной (математика описания её работы основана на простых отношениях и пропорциях) и довольно точной.

Имея стандартные сопротивления достаточной точности и нуль-детектор с необходимой чувствительностью, достижимая точность измерения сопротивления может быть не хуже +-0,05% при использовании моста Уитстона. Это метод измерения сопротивления предпочитают использовать в калибровочных лабораториях из-за его высокой точности.

Существует много вариаций основной схемы моста Уитстона. Большинство мостов постоянного тока используются для измерения сопротивления, в то время как мосты переменного тока могут быть использованы для измерения различных электрических величин, таких как индуктивность, ёмкость и частота.

Интересным вариантом моста Уитстона является двойной мост Кельвина, используемый для измерения очень малых сопротивлений (обычно менее 1/10 Ома), его схема изображена на следующем рисунке:

Низкоомные резисторы на рисунке изображены толстой линией, так же как и проводники, соединяющие их с источником напряжения, обеспечивающим сильный ток. Принцип работы этого измерительного моста причудливой конфигурации, пожалуй, лучше всего понять, если начать объяснение принципа его работы со стандартного моста Уитстона, настроенного для измерения низкого сопротивления, этот мост развивался шаг за шагом до его нынешнего состояния в попытке преодолеть некоторые проблемы, возникшие в мосте Уитстона стандартной конфигурации.

Если бы мы использовали стандартный мост Уитстона для измерения небольших сопротивлений, то его схема бы выглядела примерно так:

Когда нуль-детектор указывает нулевое напряжение, мы знаем, что мост сбалансирован и что соотношение R_a/R_x и R_M/R_N математически равны друг другу. Зная значения R_a, R_M, and R_N поэтому мы имеем все необходимые данные, чтобы найти величину Rx. Почти.

Имеется проблема в том, что соединения и соединительные провода между R_a и R_x обладают неким сопротивлением, и эти паразитные сопротивления могут быть существенными по сравнению с низким сопротивлением R_a и R_x. Эти паразитные сопротивления понизят реальное напряжение, учитывая большой ток, протекающий через них, и таким образом будут влиять на показания детектора нуля и на баланс моста:

Так как мы не хотим измерять сопротивление этих паразитных проводников и сопротивление соединений, а нас интересует только измерение сопротивления R_x, то надо найти такой способ включения нуль-детектора, что бы на его показания не влияли падения напряжений, протекающего через эти сопротивления. Если мы присоединим нуль-детектор и плечи отношений R_M/R_N напрямую к выводам R_a и R_x, то это приведёт нас к такой реализации измерительного моста:

Теперь два крайних падения напряжения E_пров. не оказывают воздействия на нуль-детектор и не влияют на точность измерений сопротивления R_x. Но два оставшихся падения напряжений E_пров. являются проблемой, так как проводник, соединяющий нижний по схеме вывод R_a и верхний по схеме вывод R_x теперь шунтирует оба падения напряжения и по нему будет течь существенный ток, который создаст на этом проводнике своё падение напряжения.

Зная, что левая часть нуль-детектора должна быть подключена к двум крайним выводам сопротивлений R_a и R_x, что бы не вносить ошибки, связанные с паразитными падениями напряжения E_пров. в цепи нуль-детектора, и что любой прямой провод, соединяющий выводы этих сопротивлений R_a и R_x будет сам нести значительный ток и создавать ещё большее паразитное падение напряжения, то единственным способом преодолеть эту проблему является создание соединения, имеющее существенное сопротивление, между нижнем по схеме выводом R_a и верхнем по схеме выводом R_x:

Справится с паразитными падениями напряжений между выводами сопротивлений R_a R_x можно путём изменения сопротивления двух новых резисторов таким образом, что бы отношение их величин было бы таким же, как и отношение величин сопротивлений в плече отношений, находящихся по схеме с правой стороны от нуль-детектора. Вот почему эти резисторы были помечены R_m и R_n в оригинальной схеме двойного моста Кельвина: для обозначения их соразмерности с сопротивлениями R_M и R_N:

При отношении R_m/R_n равном отношению R_M/R_N, резистор в плече реостата R_a регулируется до тех пор, пока нуль-индикатор не покажет, что мост сбалансирован, и тогда можно будет сказать, что отношение R_a/R_x равно отношению R_M/R_N, или просто найти R_x из следующего уравнения:

Полное уравнение баланса двойного моста Кельвина выглядит следующим образом (R_пров. – это сопротивление толстых соединительных проводов между низкоомным образцовым сопротивлением R_a и испытуемым сопротивлением R_x):

До тех пор пока соотношение между R_M и R_N равно отношению между R_m и R_n, уравнение баланса будет не сложнее чем у обычного моста Уитстона, при R_x/R_a равном R_N/R_M, так как последнее выражение в уравнении будет равно нулю, так что будет отсутствовать влияние всех сопротивлений, кроме R_x, R_a, R_M, и R_N.

Во многих двойных мостовых схемах Кельвина R_M=R_m и R_N=R_n. Однако чем меньше значения сопротивлений R_m и R_n, тем более чувствительным должен быть нуль-детектор, потому что там будет меньше последовательное сопротивление. Увеличение чувствительности детектора является полезным, так как оно позволит обнаруживать слабые дисбалансы, и таким образом мост можно будет сбалансировать с большой точностью. Таким образом некоторые высокоточные двойные мосты Кельвина используют сопротивления R_m и R_n со значениями в 100 раз меньше, чем значения сопротивлений R_M и R_N в другом плече. К сожалению, однако, чем ниже значения сопротивлений R_m и R_n, тем больший ток по ним будет течь, что увеличит влияние любого сопротивления в точке подключения R_m и R_n к R_a и R_x. Как вы можете видеть, высокая точность инструмента требует, чтобы учитывались все ошибки различных факторов, и часто лучшее, что может быть достигнуто является компромиссом минимизации двух или более различных видов ошибок.

Измерительные мосты постоянного и переменного тока. Принципы измерений: мост Уитстона

При обслуживании металлических кабельных линий наиболее часто пользуются измерительными мостами, хотя для поиска мест повреждения кабеля существуют и другие приборы. Во-первых, они обеспечивают высокую точность в широком диапазоне измеряемых величин. Во-вторых, их применение позволяет организовать измерения таким образом, чтобы компенсировать посторонние влияния, что незаменимо для локализации неисправности. В-третьих, они недороги.

Учитывая сказанное, полезно ознакомиться не только с устройством измерительных мостов, но и с принципами их применения для локализации неисправностей. Впрочем, говоря языком математики, для построения оптимальных схем измерения такие знания необходимы, но недостаточны. Диагностика — это всегда и опыт, и искусство.

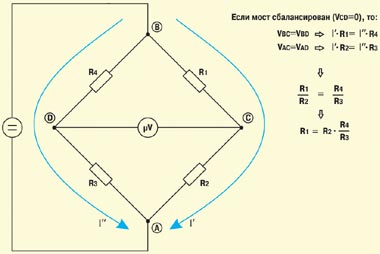
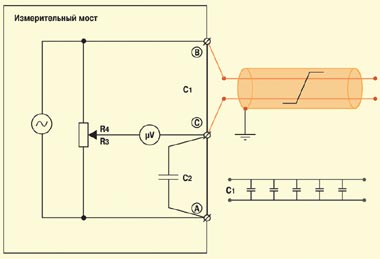
Принцип работы мостовой схемы измерения продемонстрировано на Рисунке 1 (RM1a), а способ ее применения на практике — на Рисунке 2 (RM2a). Сопротивление R1 вычисляется исходя из полученного при балансировке моста соотношения R4/R3, в качестве R2 используется резистор с известным значением. Конечно, сказанное дает только самое общее представление об измерительной схеме моста. На самом деле он устроен гораздо сложнее — современные мосты создаются на основе цифровых процессоров. Микропроцессорное ядро позволяет автоматизировать процедуру измерения (в первых моделях оператор должен был пользоваться калькулятором, сегодня же все расчеты выполняются аппаратурой), обеспечить многофункциональность устройства (многие мосты интегрированы с другими измерительными приборами — мультиметрами, рефлектометрами и т. п.), устранить помехи (посторонние постоянные и переменные напряжения почти всегда присутствуют на жилах кабелей), организовать дальнейшую обработку накопленных результатов измерений (хранение, обмен с компьютером, печать протоколов) и др.

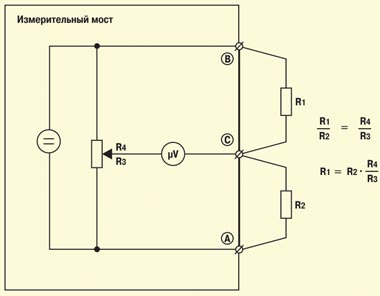
Рассмотренный выше мост, используемый для измерения сопротивления, носит имя Уитстона (Wheatstone). Для подключения измеряемых цепей в нем применяются всего две клеммы (B и C). Более сложные схемы реализованы в двух других мостах — Муррея (Murray) и Купфмюллера (Kupfmuller) (RM2в). Здесь измеряемые цепи подключаются с помощью трех клемм (A, B и C). В более сложных схемах Хиборна/Графа (Hilborn/Graf) задействуются четыре клеммы (A, B, B’ и C) (RM3). Смысл увеличения числа точек подключения станет понятен при рассмотрении схем измерения с применением мостов.

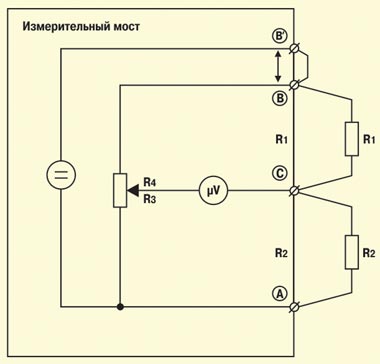
Еще один момент. Все упомянутые мостовые схемы используются для измерений при постоянном токе (определяются величины активных сопротивлений, подключенных к клеммам). Кроме того, мостовые схемы Уитстона и Муррея используются для измерений при переменном токе (определяются величины емкостей, подключенных к клеммам). В таких мостах источником напряжения служит генератор синусоидального напряжения.

Теперь остановимся на схемах измерений. С помощью моста Уитстона при постоянном токе измеряют сопротивление витой пары (шлейфа), сопротивление изоляции жил пары, сопротивление изоляции между жилами и экраном (RM3, RM4, RM5).

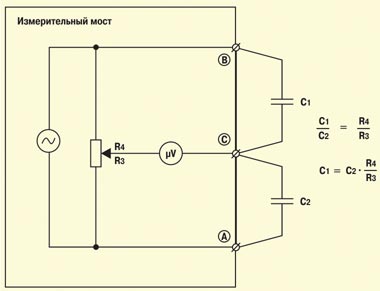
Значения упомянутых параметров используются для диагностики кабельных линий. Локализация же неисправностей требует определения места повреждения на кабельной линии. При помощи моста постоянного тока несложно вычислить расстояние до места повреждения. Зная сопротивление шлейфа Rшл и погонное сопротивление жил кабеля Rпог, можно воспользоваться формулой: Lпары = Rшл / 2Rпог, и рассчитать длину витой пары.

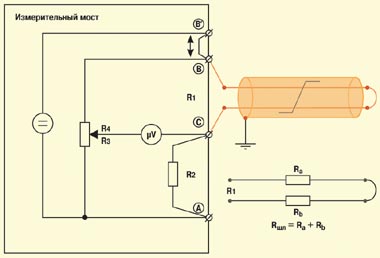
Погонное сопротивление медных жил определяется табличным способом по их сечению. Оно зависит не только от сечения жил, но и от их температуры. Чтобы избежать ошибки, нужно использовать значение погонного сопротивления для соответствующей температуры (особенно важно это для воздушных кабельных линий, где температура меняется в широких пределах). В простых мостах значения вводятся оператором вручную из таблиц. В более сложных приборах при помощи автоматической или полуавтоматической калибровочной процедуры определяется поправочный коэффициент по измеренному значению температуры (для чего в комплекте прибора присутствует щуп-датчик).

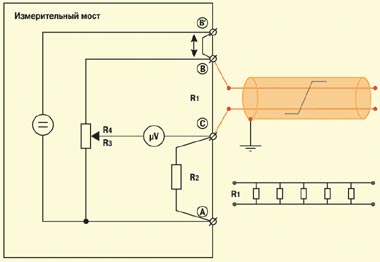
Длина витой пары может быть установлена также мостовым методом при переменном токе. В таком случае измеряемым параметром является емкость витой пары. Разделив емкость витой пары на ее погонную емкость, получим длину витой пары.

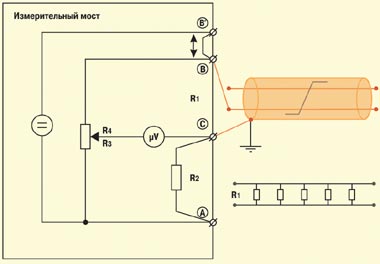
Аналогично рассмотренным выше измерениям при постоянном токе, с помощью моста Уитстона при переменном токе определяются емкость витой пары (шлейфа) и емкость каждой из жил пары относительно экрана. Длина жил может быть вычислена по их погонной емкости. Погонная емкость (нФ/км) витой пары зависит от сечения жил, типа скрутки, вида и материала изоляции и определяется табличным способом по типу кабеля.

Резкое увеличение емкости витой пары по сравнению с ее паспортным значением, как правило, свидетельствует о наличии воды в сердечнике кабеля. Для локализации повреждений этого типа применяются другие методы, прежде всего зондирование поврежденной пары с помощью рефлектометра.